A HIPÓTESE DE RIEMANN E A INTERNET (I)

 Em 1740, o matemático suíço Leonhard Euler (1707-1783) introduziu a função Zeta:

  .

A função Zeta é uma série infinita que converge para todo número real s > 1 e Euler demonstrou que ela se expressa como um produto infinito convergente, atualmente conhecido como produto de Euler,

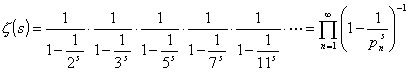
 onde o produto é tomado sobre todos os números primos p_n. Sendo assim temos:

  .

Em 1859 o matemático alemão Bernhard Riemann, um dos pioneiros da matemática atual, tratou a função Zeta como uma função de uma variável complexa z. Por esse motivo, a função é conhecida como função Zeta de Riemann.

A função Zeta não possui zeros na região do plano complexo onde Re(z)  1;              se        Re(z)  0     os seus zeros são z =  - 2, - 4, - 6,...; e ela possui infinitos zeros, chamados  zeros não-triviais, na região do plano complexo 0 < Re(z) < 1.

Riemann conjecturou que os zeros não triviais se encontram na reta Re(z) = ½.

Essa conjectura é chamada de Hipótese de Riemann. A demonstração do Teorema do Número Primo por Hadamard e de la Vallée-Poussin, em 1896,  tinha um raciocínio crucial mostrando que  quando Re(z) = 1, ou seja, a função Zeta não possui zeros na reta  Re(z) = 1.

Em 1914, o brilhante matemático britânico Godfrey Hardy  demonstrou que infinitos zeros da função Zeta se encontram na reta Re(z) = ½. Sabe-se que os primeiros 1,5.10⁹ zeros na região 0 < Re(z) < 1 estão todos na reta Re(z) = ½. Entretanto, aguarda-se uma demonstração da Hipótese de Riemann.

Essa conjectura é considerada um dos maiores e mais interessantes problemas em aberto de toda a Matemática, pois, além de revelar um conhecimento profundo da distribuição dos números primos, ela também está relacionada a um dos problemas atuais da maior importância: a segurança na internet.

Quando escrevemos uma carta de instruções para compra de ações, ou fazemos uma transação bancária em um caixa eletrônico, dependemos do conhecimento matemático sobre o comportamento dos números primos, para manter a segurança do sistema.

Por outro lado uma demonstração da Hipótese de Riemann poderia levar a grandes conquistas na investigação da fatoração de números grandes e colocar em perigo as técnicas utilizadas atualmente para manter a segurança da rede mundial de computadores.

A questão de se manter uma mensagem secreta, de tal forma que somente o destinatário almejado possa compreendê-la, é um problema antigo, especialmente se pensarmos em questões militares, diplomáticas ou comerciais. A maneira encontrada, para que alguém não autorizado que tenha acesso a uma mensagem não a compreenda, foi cifrá-la.

A criptologia é a disciplina que lida com os sistemas sigilosos e as suas origens remontam à Antiguidade Clássica, quando os gregos propuseram a seguinte solução: um escravo mensageiro tinha os seus cabelos raspados e a mensagem copiada em seu couro cabeludo. Após o crescimento do cabelo, ele era mandado ao destino da mensagem. O destinatário raspava o cabelo do escravo e lia a mensagem. É claro que sempre havia a possibilidade de o escravo ser interceptado pelo inimigo.

O imperador romano Júlio César propôs uma outra solução, denominada atualmente de cifra de César, para tornar secretas as mensagens que enviava para seus generais em missões na Europa. 

A mensagem escrita era modificada de modo que cada letra da mensagem era transformada em três letras seguintes do alfabeto latino e as três últimas letras correspondiam às primeiras do alfabeto da seguinte maneira: D corresponderia a A, E corresponde a B, ... , Y corresponderia a V, ... , A corresponderia a X, ... , C corresponderia a Z.

Dessa maneira, a famosa frase de Júlio César “VENI.VIDI.VICI.” (“Vim. Vi. Venci.”) tornava-se “YHQL.YGLG.YLFL.” Júlio César inventou, portanto, um dos primeiros cripto-sistemas.

A criptografia é uma disciplina dentro da criptologia que lida com o projeto e implementação de sistemas sigilosos e a cripto-análise é a disciplina que lida com a decifração desses sistemas sigilosos.

Cifrar é o procedimento de transformar uma mensagem em um texto cifrado. Ou seja, modificam-se as letras da mensagem por meio de uma transformação especificada. A chave determina uma transformação particular de um conjunto de transformações possíveis.

O processo inverso de cifrar é conhecido como decifrar ou decifração. O destinatário desejado da mensagem possui o método para fazer a sua decifração. Esse processo é diferente do processo que alguém, que não seja o destinatário desejado, utiliza para tornar a mensagem inteligível, processo chamado de cripto-análise.

Um cripto-sistema é constituído de um conjunto de mensagens admissíveis, um conjunto de mensagens cifradas possíveis, um conjunto de chaves, onde cada chave especifica uma função criptografia particular, e as suas correspondentes funções decifração.

Devido à possibilidade de se interceptar mensagens e decifrá-las, houve um esforço muito grande, por parte dos cientistas, para se desenvolver métodos seguros. Em geral, nos cripto-sistemas atuais,     o procedimento de cifrar consiste em um programa computacional, ou um chip, e uma chave consiste em um número escolhido secretamente.

A chave escolhida é imprescindível para cifrar a mensagem e o texto cifrado resultante só poderá ser decifrado com o auxilio de outra chave secreta e exclusiva de um único usuário do cripto-sistema. Dessa forma, o programa que cifra pode ser usado por muitas pessoas e por um certo período de tempo, pois a segurança é “garantida” pela chave secreta e exclusiva.          

Nos primeiros sistemas com chave, as pessoas que desejavam comunicar-se possuíam uma chave comum. Essa condição trouxe algumas desvantagens. Por exemplo, as transações comerciais ou bancárias envolvendo pessoas de diferentes partes do globo se mostraram inviáveis, pois, para manter o sistema seguro, as pessoas tinham que concordar quanto a uma chave comum, mas como se comunicar secretamente para escolher a chave?

Na década de 70, a noção de chave pública criptográfica foi introduzida e com                   o desenvolvimento dos cripto-sistemas de chave pública houve um grande progresso. As principais características desse sistema são a chave pública, a simplicidade e a eficiência, pois, a dificuldade para se violar uma mensagem cifrada é muito grande. Essa idéia foi proposta em 1976 pelos matemáticos Whitifield Diffie e Martin Hellman.

Na criptografia de chave pública, duas chaves são exigidas, uma para cifrar e outra para decifrar. Suponhamos que um novo usuário X obtenha o programa padronizado usado por todos os membros de uma certa rede. O usuário X gera duas chaves: uma chave para decifrar mensagens, que ele mantém secreta, e uma outra chave que ele utiliza para cifrar mensagens a serem enviadas para ele por qualquer outra pessoa da rede. Essa última ele publica em um diretório dos usuários da rede.

Sendo assim, para enviar uma mensagem a X, o que se deve fazer é procurar a chave pública dele, cifrar a mensagem, usando essa chave, e enviá-la. Para decifrar a mensagem não basta conhecer a chave pública, que inclusive está disponível para qualquer pessoa. É necessário, também, conhecimento da chave que a decifre, que é conhecida apenas por X.

Inúmeros métodos foram desenvolvidos para se implementar a idéia de Diffie e Hellman, porém, a que recebeu maior apoio e que permanece até hoje como padrão foi obtida por Rivest, Shamir e Adleman. Esse cripto-sistema, denominado RSA devido às iniciais de seus autores, é o sistema criptográfico de chave pública mais utilizado.                  

A segurança é baseada na fatoração de números inteiros. X escolhe dois números primos p e q, cada um tendo pelo menos 100 dígitos. Esses primos são gerados aleatoriamente por computadores para que não haja violação do sistema. A chave secreta de decifração consiste nesses dois números primos.     A chave pública que cifra é o produto n = pq desses primos. Como não há método rápido para se fatorar completamente números inteiros grandes, o sistema se mantém seguro porque, como ninguém consegue descobrir p e q, digamos, em menos de um  ano, dá tempo de terminar a transação sem a interferência de intrusos.

Na próxima coluna voltaremos a esse tema apaixonante quando introduziremos a aritmética modular necessária para se entender com mais detalhes o cripto-sistema RSA.